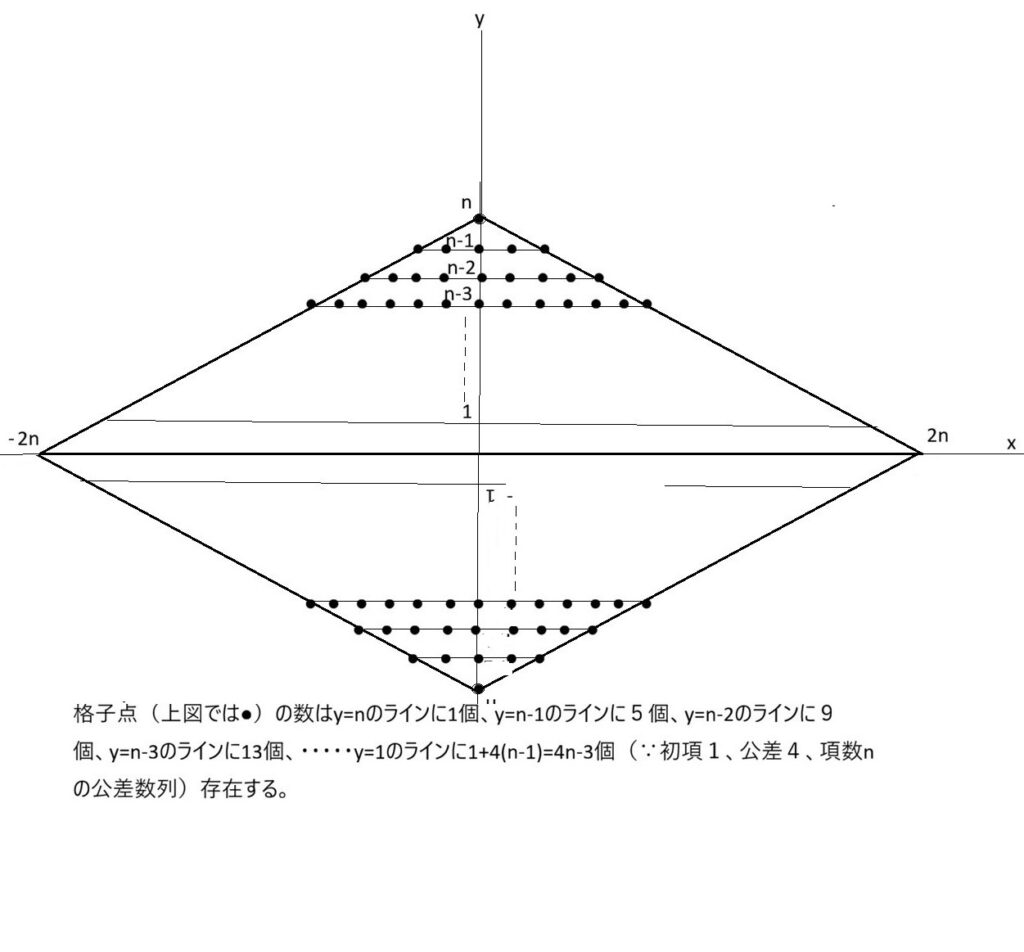
$上図と脚注から、y=1からy=nまでの間に存在する格子点の数は$
$\displaystyle \sum_{k=1}^n (4k-3)$
$=4\cdot\displaystyle\frac{n(n+1)}{2}-3n$
$=2n^2-n-①$
$y=-1からy=-nまでの間にも同数が存在する。-②$
$また、y=0上には2n+2n+1(原点)=4n+1の格子点がある。-③$
$即ち、①②③から|x|+|2y|≦2nを満たす格子点の総数は、$
$2(2n^2-n)+4n+1$
$=4n^2+2n+1$
$※なお、前問はn=2のときであるから、$
$格子点は4\cdot 2^2+2\cdot 2+1=21$