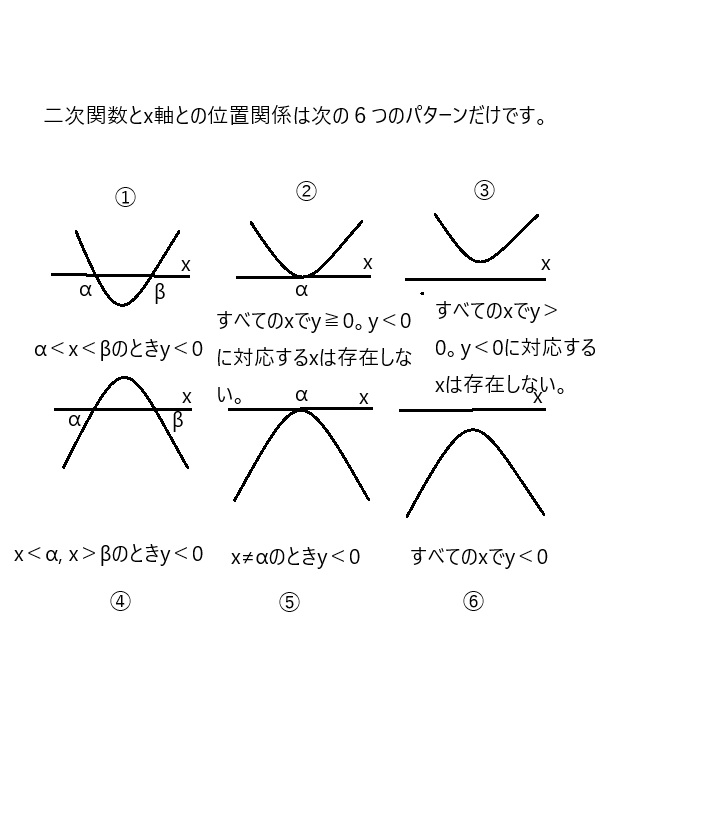
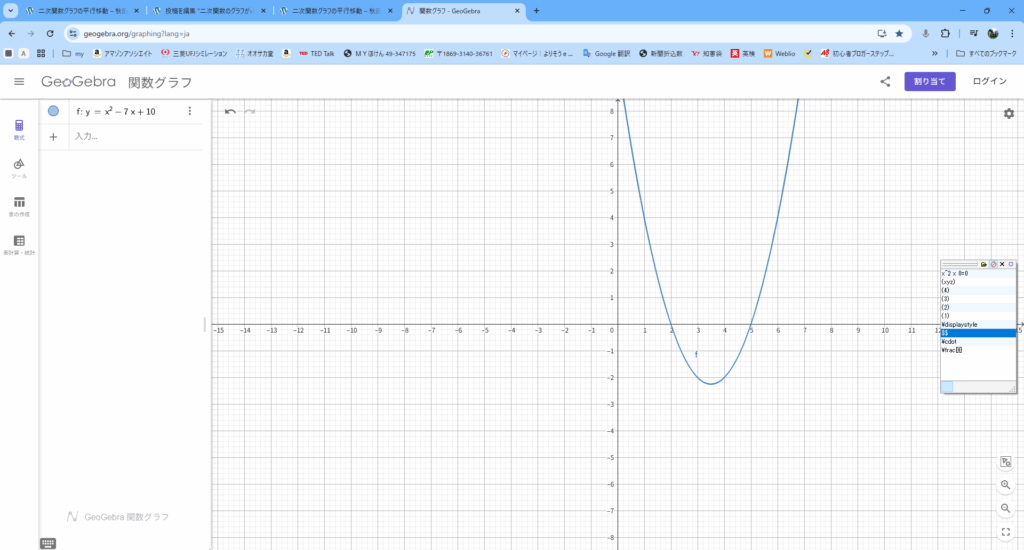
1(1)
$f(x)=y=x^2-2x+26-①$のグラフを原点に関して対称移動したグラフを$g(x)$、$f(x)$上の任意の座標を$(X,Y)$、$(X,Y)$を原点に関して対称移動した$g(x)$上の座標を$(x,y)$とする。
座標を原点に対して対称移動すると符号が入れ替わるので、$x=-X, y=-Y$であるが、$X=-x, Y=-y$と表すこともできる。
ここで、$(X,Y)$は$f(x)$上の座標であることから、$(X,Y)$の代わりに$(-x,-y)$を①の式に代入しても等式は成り立つ。
即ち$-y=(-x)^2-2(-x)+26$。
整理して、$g(x)=y=-x^2-2x-26$
別解
$f(x)=y=x^2-2x+26=(x-1)^2+25$であるから頂点は$(1,25)$であり原点について対称移動すると$(-1,-25)$。
$(-1,-25)$を頂点とし、$x^2$の係数が$-1$であるグラフは、$y=-(x+1)^2-25=-x^2-2x-26$
(2)
$g(x)$を$x$軸方向に$\displaystyle-\frac{1}{2}$移動したグラフを$h(x)$、$g(x)$上の任意の座標を$(X,Y)$、$(X,Y)$を$x$軸方向に$\displaystyle-\frac{1}{2}$移動した$h(x)$上の座標を$(x,y)$とする。
$X-\displaystyle\frac{1}{2}=x$より、$(X,Y)=(x+\displaystyle\frac{1}{2},y)$であり、$(X,Y)$は$g(x)$上の座標であるから、
$g(x+\displaystyle\frac{1}{2})=h(x)=-(x+\displaystyle\frac{1}{2})^2-2(x+\displaystyle\frac{1}{2})-26$が成り立つ。
整理して、$h(x)=-x^2-x-\displaystyle\frac{1}{4}-2x-1-26$
$=-x^2-3x-\displaystyle\frac{109}{4}$
別解
$移動先のグラフの任意の点を(x,y)とすると、$
$移動元の座標は(x+\displaystyle\frac{1}{2},y)である。$
この座標は、
$y=-x^2-2x-26$
上の座標であるから、
$y=-(x+\displaystyle\frac{1}{2})^2-2(x+\displaystyle\frac{1}{2})-26が成り立つ。$
$※グラフ上の任意の座標はそのグラフの方程式を満たす$
$(=変数に代入すると等式が成り立つ)$
(3)
$I(x)=y=x^2+3x+12=(x+\displaystyle\frac{3}{2}x)^2+\displaystyle\frac{39}{4}$から最小値は$\displaystyle\frac{39}{4}$
また、$h(x)=y=-(x^2+3x)-\displaystyle\frac{109}{4}=-(x+\displaystyle\frac{3}{2})^2-25$から最大値は$-25$
$-25$と$\displaystyle\frac{39}{4}$の中点は$(-25+\displaystyle\frac{39}{4})×\displaystyle\frac{1}{2}$
$=-\displaystyle\frac{61}{8}=a$
2
軸が$x=2$である放物線は$y=a(x-2)^2+b$
したがって、$0=9a+b$かつ$10=4a+b$
∴ $a=-2, b=18, c=-2×4+18=10$
3
グラフは下に凸だから$f(0)$が最小値になるのは、軸$x=-\displaystyle\frac{a}{2}≦0、即ちa≦0$のとき。
$y=(x+1)^2-3=x^2+2x-2$
4
(1)
$f(x)=x^2-ax-a^2=(x-\displaystyle\frac{a}{2})^2-\displaystyle\frac{5a^2}{4}$ (0≦x≦4)
軸は$x=\displaystyle\frac{a}{2}$
$\displaystyle\frac{a}{2}<0$、即ちa<0のとき、最小値$f(0)=-a^2$
$0≦\displaystyle\frac{a}{2}≦4$のとき、即ち$0≦a≦8$のとき、$f(\displaystyle\frac{a}{2})=\displaystyle\frac{5a^2}{4}$
$\displaystyle\frac{a}{2}>4$、即ちa>8のとき、最小値$f(4)=-a^2-4a+16$
(2)
$\displaystyle-\frac{a}{2}<2$のとき、即ち$a>-4$のとき、最大値$f(4)=-a^2-4a+16$
$\displaystyle-\frac{a}{2}=2$のとき、即ち$a=-4$のとき、最大値$f(0)=f(4)=-16$
$\displaystyle-\frac{a}{2}>2$のとき、即ち$a<-4$のとき、最大値$f(0)=-a^2$
よって、与えられた条件から最大値が11になるのは$-a^2-4a+16=11$のとき。
$a^2+4a-5=0$を解いて$a=-5,1$
5
$3y^2=2-2x^2$
$y^2≧0であるから2-2x^2≧0より2(x-1)(x+1)≦0、即ち-1≦x≦1$
$x^2+x+3y^2$
$=x^2+x+(2-2x^2)$
$=-x^2+x+2$
$=-(x-\displaystyle\frac{1}{2})^2+\displaystyle\frac{9}{4}$
$x=\displaystyle\frac{1}{2}のとき最大値\displaystyle\frac{9}{4}$
$x=-1のとき最小値-1-1+2=0$]
6
$y=a(x^2-6x)+5a+6$
$=a(x-3)^2-4a+6$
題意より、
$-4a+6=-6$
$a=3$
このとき、$y=3x^2-18x+21$
$x軸との交点をα,βとするとα+β=6, αβ=7-①。$
このグラフがx軸から切り取る部分の長さは、
交点間の距離に等しく$\sqrt{(α-β)^2}$である。
$\sqrt{(α-β)^2}$
$=\sqrt{(α+β)^2-4αβ}$
$=\sqrt{6^2-4\cdot7}$
$=\sqrt{8}$
7
$x^2+2ax+6a=0の判別式はa^2-6a=a(a-6)$
$この方程式が実数解を持つのはa(a-6)≧0、即ちa≦0, a≧6のとき。-①$
$この方程式が実数解を持たないのはa(a-6)<0、即ち0<a<6のとき。-②$
$一方、x^2-2ax-5a+6=0の判別式はa^2+5a-6=(a+6)(a-1)$
$この方程式が実数解を持つのは(a+6)(a-1)≧0、$
$即ちa≦-6, a≧1のとき。-③$
$この方程式が実数解を持たないのは(a+6)(a-1)<0、$
$即ち-6<a<1のとき。-④$
どちらか一方だけが実数解をもつのは①かつ④または②かつ③のとき、
$即ち-6<a≦0, 1≦a<6のときである。$
8
$f(x)=x^2-2ax-aとすると、$
$①D>0, ②f(-1)>0, ③f(1)>0, ④-1<軸<1が同時に成り立つ。$
$なお、②③が成り立つ理由は、-1<x軸との交点<1だから。$
$D/4=a^2+a=a(a+1)>0からa<-1, a>0-①$
$f(-1)=1+2a-a=a+1>0からa>-1-②$
$f(1)=1-2a-a=-3a+1>0からa<\displaystyle\frac{1}{3}-③$
$-1<a<1-④$
$①②③④から、0<a<\displaystyle\frac{1}{3}$
9
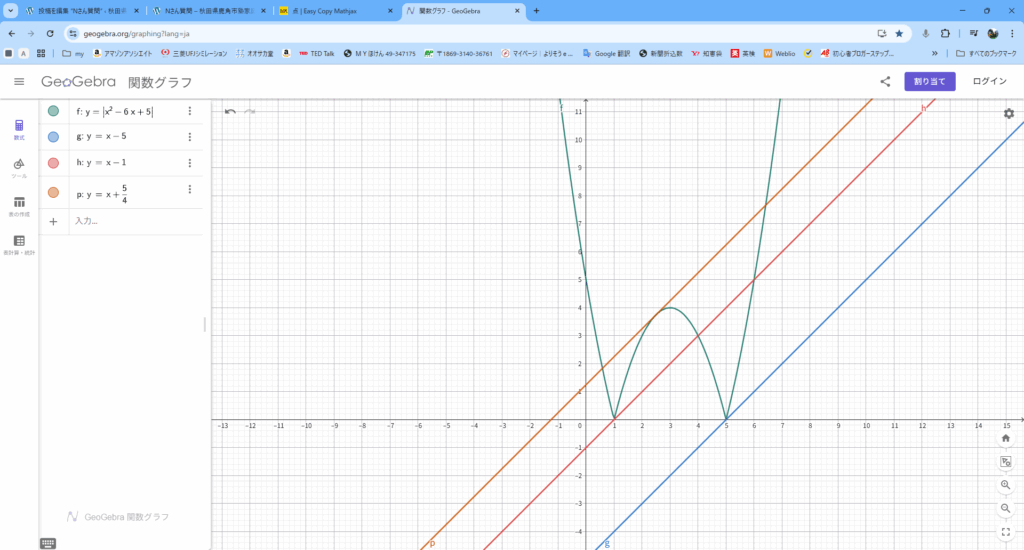
傾きが1で、
$(5,0)を通る直線はy=x-5$
$(1,0)を通る直線はy=x-1$
$y=-x^2+6x-5とy=x+mが接する条件は、$
連立方程式の判別式が0になることであるから、
$-x^2+6x-5-x-m=-x^2+5x-5-m=0$
$x^2-5x+5+m=0よりD=25-20-4m=0$
$即ちこのときm=\displaystyle\frac{5}{4}$
$図から2点で交わるようなmの値は、$
$-5<m<-1, m>\displaystyle\frac{5}{4}$
10
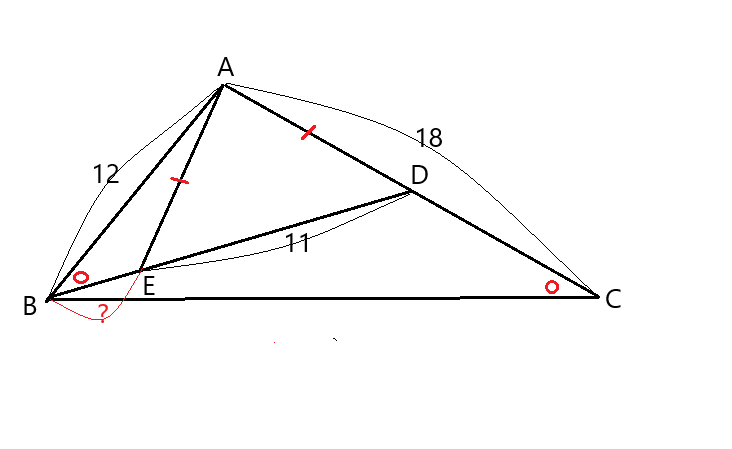
$方程式x^2-2ax-3a+4=0の解の一つが-1であることから、$
$1+2a-3a+4=0からa=5$
$このとき方程式はx^2-10x-11=0となる。$
$解と係数の関係から、-1+もう一つの解=10であり、$
イは11であることがわかる。
$f(x)=x^2-2ax-3a+4$とすると、
$f(x)≦0が解を持たないのはf(x)の最小値が0より大きいときであるから、$
$f(x)=(x-a)^2-a^2-3a+4から-a^2-3a+4>0$
$a^2+3a-4=(a+4)(a-1)<0、即ち-4<a<1のときである。$
$|x|≦1、即ち-1≦x≦1を満たす実数xがすべてf(x)≦0を満たすためには$
$-1≦x≦1がf(x)≦0を満たす解の内側に(境界線を含めて)$
$収まっているときであるから$
$f(-1)≦0, f(1)≦0のときである。$
$f(-1)=1+2a-3a+4=-a+5≦0よりa≧5-①$
$f(1)=1-2a-3a+4=-5a+5≦0よりa≧1-②$
$①②から5≦a $